Introduction
H-infinity optimization is a powerful modern tool. It allows the design of high-performance and robust control systems. The Polynomial Toolbox offers two routines for H-infinity design:

• Mixed sensitivity optimization of SISO systems relying on transfer function descriptions.
• A routine dsshinf for finding all suboptimal solutions of the general standard HY optimization problem based on descriptor representations
• A very comprehensive routine dssrch for finding optimal solutions of the general standard H Ą optimization problem based on descriptor representations.

SISO Mixed Sensitivity
The SISO mixed sensitivity problem consists of minimizing the square root of

where

are the sensitivity and input sensitivity functions of the closed-loop system of Fig. 1, respectively.

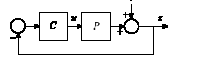
Figure 1

The rational function

is a shaping filter, and the rational functions

are weighting filters.

The SISO mixed sensitivity problem is solved by the command

[y,x,gopt]=mixeds(n,m,d,a1,b1,a2,b2,gmin,gmax, accuracy)

The input parameters gmin and  gmax are lower and upper bounds for the minimal value of the mixed sensitivity criterion, respectively. The parameter accuracy specifies how closely the minimal norm is to be approached.

Standard H-infinity optimization problem
Besides the mixed-sensitivity SISO optimization, routines for the solution of the standard H-infinity optimization problem are included in the Polynomial Toolbox 2.0. The corresponding routines are named dsshinf and dssrch.

The former looks for a sub-optimal solution with a pre-scribed value of the infinity norm, while the latter seeks the H-infinity optimal solution by binary search and repeated calls of dsshinf.

All the macros introduced above are thoroughly described in the Polynomial Toolbox 2.0 for Matlab Manual, along with the overview of the theory standing behind and illustrative examples.