Modern control theory addresses various problems involving uncertainty. A mathematical model of a system to be controlled typically includes uncertain quantities. In a large class of practical design problems the uncertainty may be attributed to certain coefficients of the plant transfer matrix. The uncertainty usually originates from various physical parameters whose values are specified only within given bounds. An ideal solution to overcome the uncertainty is to find a robust controller — a simple, fixed controller, designed off-line, which guarantees desired behavior and stability for all expected values of the uncertain parameters.

The Polynomial Toolbox offers several simple tools that are useful for robust control analysis and design for systems with parametric uncertainties. The relevant macros are briefly introduced in this chapter.

Single Parameter Uncertainty
Many systems of practical interest involve a single uncertain parameter. At the time of design the parameter is only known to lie within a given interval. Quite often even more complex problems (with a more complex uncertainty structure) may be reduced to the single parameter case. Needless to say that the strongest results are available for this simple case. Even though the uncertain parameter is single it may well appear in several coefficients of the transfer matrix at the same time. Quite in the spirit of the Polynomial Toolbox the coefficients are assumed to be polynomial functions of the uncertain parameter and can be naturally passed to the macro stabint which returns the margins within which the family thus described remains stable.

Interval Polynomials
Another important class of uncertain systems is described by interval polynomials with independent uncertainties in the coefficients. In many applications interval polynomials arise when an original uncertainty structure is known but too complex (e.g., highly nonlinear) to be tractable but can be ”overbounded” by a simple interval once an independent uncertainty structure is imposed. Using the Polynomial Toolbox, it is convenient to describe interval polynomials by their ”lower” and ”upper” elements.

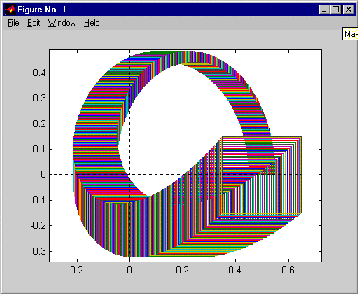
Two basic approaches can be employed when testing the stability of interval polynomials by means of the Polynomial Toolbox. The former is the famous Kharitonov test that is implemented in the kharit function. Alternatively, one can call the macro khplot and test the stability robustness by viewing the value sets for particular frequencies and taking the zero exclusion condition into account. An example of related figure for a particular choice of interval plant is given below.

Polytopes of Polynomials
A more general class of systems is described by uncertain polynomials that linearly depend on several parameters, but where each parameter may occur simultaneously in several coefficients. Uncertain polynomials with the affine uncertainty structure form polytopes in the space of polynomials.

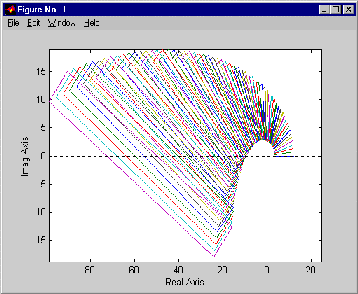
The Version 2 of the Polynomial Toolbox also counts with uncertainty structure of this kind. In general, the value set concept and zero exclusion condition introduced before for the interval polynimials remain valuable also in this case and the macro ptopplot has been included in the package to compute and display related graphs.